Drittmittelprojekte

DFG Logo

Foto: DFG

Das Verständnis und die Quantifizierung der Komplexität zeitabhängiger Systeme nimmt in der Theorie dynamischer Systeme eine zentrale Rolle ein. Der Begriff der Entropie ermöglicht es dabei, die einem System inherente "Chaotizität" zu messen. Auch bei verschwindender Entrope lässt sich allerdings eine bemerkenswerte Vielfalt an dynamischen Verhaltensweisen beobachten. Daher ist die Untersuchung von Null-Entropie-Systemen ein Gebiet von eigenständigem Interesse, das in den letzten Jahrzehnten erhebliche Fortschritte verzeichnet hat. Eine besondere Motivation dafür ergibt sich aus der Theorie der aperiodischen Ordnung, bei der mathematische Modelle von Quasikristallen und andere aperiodischen Strukturen über von diesen induzierte dynamische Systeme untersucht werden. Unterschiedliche Niveaus langreichweitiger Ordnung entsprechen dann unterschiedlichen Graden dynamischer Komplexität.

Ein alternativer Zugang zur Untersuchung dynamischer Systeme besteht inder Betrachtung von Erweiterungsstrukturen. Dieser Ansatz hat zu wegweisenden Ergebnissen wie dem Furstenberg-, dem Furstenberg- Zimmer- oder dem Veech-Strukturtheorem geführt. Im Kontext von Systemen geringer Komplexität lässt sich hoffen, wichtige Systemklassen durch grundlegende Erweiterungsstrukturen charakterisieren zu können. In jüngerer Zeit gab es dabei erhebliche Fortschritte im Verständnis gleichgradig stetiger minimaler Systeme. Wie Glasner und Downarowicz zeigen, sind diese isomorph zu ihrem maximal gleichgradig stetigen Faktor (MEF), einer zugrundeliegenden kompakten Gruppenrotation, die den "regulären" (nicht-chaotischen) Teil der Dynamik codiert. Durch nachfolgende Resultate wurde eine Hierarchie von Unterklassen etabliert, die durch unterschiedliche Invertierungseigenschaften der Faktorabbildung zum MEF charakterisiert sind.

Das Projekts baut auf diesen jüngsten Fortschritten auf, um die Theorie auf eine allgemeinere Klasse von Systemen auszudehnen, die als endliche topomorphe Erweiterungen bezeichnet werden. Dies stellt einen natürlichen nächsten Schritt im Verständnis der Dynamik von geringer Komplexität aus der Perspektive von Erweiterungsstrukturen dar. Darüber erfasst dies eine Reihe paradigmatischen Beispielen aus dem Bereich der aperiodischer Ordnung (z.B. Thue-Morse oder Rudin-Shapiro). Ziel des Projekts ist es, dynamische Charakterisierungen von endlichen topomorphen Erweiterungen und wichtigen Unterklassen bereitzustellen, die wiederum in Bezug auf strukturelle Eigenschaften der MEF-Faktorabbildung definiert sind. Um die Komplexität dieser Systeme zu beschreiben und Konjugationsklassen zu unterscheiden, soll eine Familie maßgeschneiderter topologischer Invarianten etabliert werden. Darüber hinaus werden die
Konstruktion und Untersuchung neuer Beispiele eine herausragende Rolle spielen und Hand in Hand mit der Entwicklung der allgemeinen Theorie gehen

DFG GZ OE 538/13-1.

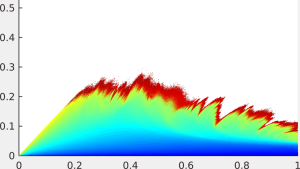
Parameterraum der getriebenen Harper-Abbildung

Foto: Tobias Jäger

 In der Theorie dynamischer Systeme kommt dem Verständnis niedrig-dimensionaler Systeme eine  wichtige Bedeutung zu, da diese oft grundlegende Mechanismen und paradigmatische Beispiele beschreiben, die in einen wesentlich größeren Kontext relevant sind. Während die Untersuchung eindimensionaler Systeme weit fortgeschritten ist, sind zweidimensionale Systeme noch wesentlich weniger verstanden und grundlegende Probleme in diesem Zusammenhang noch völlig offen. Das Ziel des Projektes war es, jüngste Entwicklungen und neu verfügbare Methoden zu nutzen, um eine Reihe von zentralen offenen Problemen in der Dynamik von 2-Mannigfaltigkeiten zu untersuchen. Hauptaugenmerk lag dabei auf der Klassifikation von Null-Entropie-Systemen, dem Übergang von Ordnung zu Chaos und der Rotationstheorie auf 2-Mannigfaltigkeiten.

Überraschende Fortschritte konnten zudem bei der Beschreibung des Diffusionsverhaltens der getriebenen Harper-AbbildungExterner Link gemacht werden, die bei der Modellierung unterschiedlicher physikalischen Situationen auftritt. 

DFG-Projekt 330226174. Externer Link

DFG Heisenberg Logo

Foto: DFG

Die Professur `Ergodentheorie und Dynamische Systeme' wurde in einer 5-jährigen Anfangsphase über das Heisenberg-Programm der DFG finanziert. In diesem Zusammenhang wurden Forschungsprojekte zu topologischen, geometrischen und probabilistischen Aspekten dynamischer Systeme durchgeführt. 

DFG-Projekte 271404167Externer Link und 407739711Externer Link.

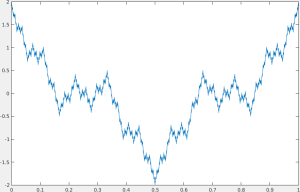
Graph der Weierstrass-Funktion.

Abbildung: Tobias Jäger

Das Ziel des wissenschaftlichen Netzwerks „Dynamik von Skew-Produkten und multifraktale Analyse“ war es, Experten aus der Theorie dynamischer Systeme und der fraktalen Geometrie zusammenzubringen, um an der Schnittstelle dieser beiden Themen zu arbeiten. Der Fokus lag dabei vor allem auf den fraktalen Strukturen von invarianten Kurven und graphenartigen Attraktoren in Schiefprodukt-Systemen lag. Ein Schlüsselelement für die Interaktion innerhalb des Netzwerks war ein Workshop-Programm mit vier Veranstaltungen, die in den Jahren 2012–2015 jährlich organisiert wurden. Diese dienten der Förderung der beteiligen Nachwuchswissenschaftler:innen und ermöglichten ihnen, fundierte Kenntnisse in verschiedenen aktuellen Themenbereichen zu erwerben. Gleichzeitig boten die Treffen die Gelegenheit zu einem fruchtbaren Austausch über die laufende Forschung der Teilnehmer:innen und zahlreiche Publikationen wurden bei diesen Veranstaltungen initiiert oder von ihnen begünstigt.

Während des Projekts wurden in mehreren Richtungen bedeutende Fortschritte erzielt. So wurde beispielsweise eine 25 Jahre alte Vermutung über die fraktale Struktur sogenannter seltsamer nichtchaotischer Attraktoren bestätigt, und es wurden Methoden entwickelt, um die Dimensionen solcher Attraktoren in breiten Systemklassen zu bestimmen. Darüber hinaus haben Mitglieder des Netzwerks eine aktive Rolle bei den jüngsten Fortschritten in der Untersuchung des klassischen Weierstraß-Graphen gespielt. Letzterer wurde von Weierstraß bereits zu Beginn des 20. Jahrhunderts als Beispiel für eine stetige, aber nirgends differenzierbare Kurve eingeführt. Eine präzise Beschreibung seiner fraktalen Struktur und Dimensionen wurde jedoch erst vor kurzem vollständig abgeschlossen. Weitere Beiträge wurden zum  Studium von Verzweigungsmustern und Blowout-Bifurkationen in getriebenen Systemen sowie zur Untersuchung der fraktale Struktur sogenannter hyperbolischer Graphen gemacht. Schließlich wurden überraschende Verbindungen zwischen der Dynamik von Schiefprodukt-Systemen und der mathematischen Theorie der Quasikristalle entdeckt und es wurde ein substanzieller und fruchtbarer Austausch von Ideen und Methoden zwischen den beiden Gebieten initiiert. Weitere Informationen finden sich im DFG-AbschlussberichtExterner Link.

DFG-Projekt 217182598Externer Link. Start 2012 an der TU Dresden, Transfer nach Jena 2015. 

Logo DFG Emmy Noether

Foto: DFG

Ergodentheorie und Dynamische Systeme haben in vielen anderen Bereichen der Mathematik und nahezu allen Wissenschaften Anwendung gefunden. Ziel des Forschungsprojekts war es, durch die Untersuchung verschiedene Arten von niedrigdimensionalen und/oder nicht-autonomen dynamischen Systemen substanzielle Beiträge zu diesem Gebiet zu leisten. Ein gemeinsames Merkmal der betrachteten Systeme ist das Fehlen oder die Irrelevanz von periodischen Orbits. Dies macht ihre Untersuchung besonders schwierig, da in der überwiegenden Mehrheit der Fälle, in denen das Langzeitverhalten eines dynamischen Systems gut verstanden wird, die Existenz periodischer Orbits ein entscheidendes Merkmal und oft der Ausgangspunkt der Analyse ist. Im Gegensatz dazu sind dynamische Systeme ohne periodische Punkte allgemein noch nicht ausreichend verstanden, so dass neue Konzepte und Ideen für ihre Beschreibung erforderlich sind. Zu den behandelnden Themen gehören insbesondere die Rolle sogenannter seltsamer nichtchaotischer Attraktoren bei der Klassifikation quasiperiodisch getriebener Kreisabbildungen, nicht-autonome Verzweigungstheorie und die Klassifikation der Dynamik von Torus-Homöomorphismen.

.DFG-Projekt 129048169Externer Link. Start 2009 an der TU Dresden, Transfer nach Jena 2015.