Strange non-chaotic attractor-repeller triplet in a nonsmooth pitchfork bifurcation.

Neues DFG-Projekt: Finite topomorphic extensions

Das von der AG Dynamische Systeme durchgeführte Projekt zielt auf eine tieferes Verständnis breiter Klassen dynamischer Systeme ab, die unter anderem bei der mathematischen Modellierung von Quasikristallen auftreten.
Strange non-chaotic attractor-repeller triplet in a nonsmooth pitchfork bifurcation.
Abbildung: Tobias Jäger
  • Mathematik

Meldung vom: | Verfasser/in: Tobias Jäger

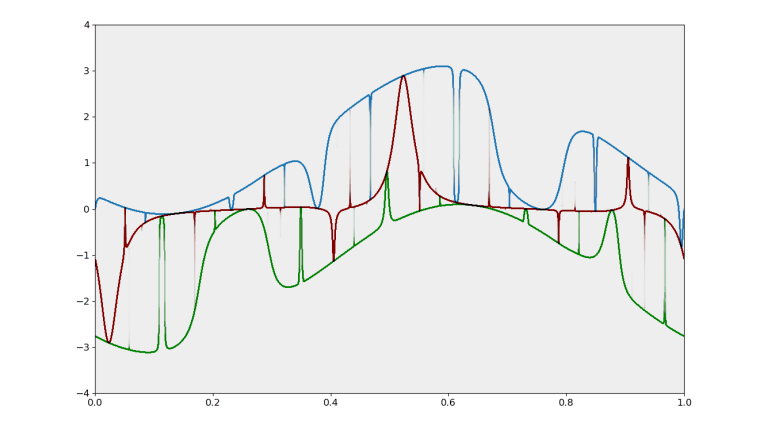
Im Fokus des ab Anfang 2025 von der DFG geförderten Projektes Finite topomorphic extensions of equicontinuous systems wird die Untersuchung breiter Klassen dynamischer Systeme im Bereich niedriger und mittlerer Komplexität stehen, die beispielsweise im Zusammenhang mit aperiodischer Ordnung (Quasikristalle), quasi-periodischen Schrödinger-Operatoren, Substitutionssystemen wie der klassischen Thue-Morse Substitution oder seltsamen nicht-chaotischen Attraktoren in nicht-glatten Verzweigungen (s. Abbildung) auftreten können.

Beteiligte Wissenschaftler

  1. Drewlo, Jamal Paul Professur für Ergodentheorie und Dynamische Systeme

    Raum 3342
    Ernst-Abbe-Platz 2
    07743 Jena

    Mitarbeiterphoto Jamal Drewlo
    Foto: Jamal Drewlo
  2. Haupt, Lino Joss Fidel Professur für Ergodentheorie und Dynamische Systeme

    Raum 3342
    Ernst-Abbe-Platz 2
    07743 Jena

  3. Kang, Zeyu Professur für Ergodentheorie und Dynamische Systeme

    Raum 3342
    Ernst-Abbe-Platz 1-2
    07743 Jena

    Porträt-Foto Zeyu Kang
    Foto: Zeyu Kang
  4. Lenz, Daniel, Univ.-Prof. Dr. Professur für Analysis

    Raum 3502A
    Ernst-Abbe-Platz 1-2
    07743 Jena

    Prof. Dr. Daniel Lenz
    Foto: Carina Linne
  5. Oertel-Jäger, Tobias, Univ.-Prof. Dr. Professur für Ergodentheorie und Dynamische Systeme

    Raum 3344
    Ernst-Abbe-Platz 1-2
    07743 Jena

    Portrait Tobias Jäger
    Foto: Anne Günther (Universität Jena)