Programmtransformationen - noch ein Eisen im Feuer haben
von Prof. Dr. H. Martin Bücker
Beispiel einer Ableitung
Kaum eine Fragestellung aus Wissenschaft, Wirtschaft oder Gesellschaft wird heute ohne die Hilfe eines Computers beantwortet. Die Liste der möglichen Anwendungsgebiete, in denen computergestützte Verfahren zur Simulation und Datenanalyse erfolgreich eingesetzt werden, wächst ins Uferlose: Hirnsignale werden in Wörter übersetzt, Fahrzeugtypen werden auf ihre Ökobilanzen hin analysiert, elektrischer Strom wird aus der Luft entnommen, …
Der Informatik kommt in diesen Anwendungsgebieten die wichtige Rolle zu, aus konkreten Einzelfragestellungen die zugrundeliegenden allgemeinen Problemstrukturen zu bestimmen und schließlich effiziente Lösungsansätze zu entwickeln und in der Praxis umzusetzen. In einer solchen Vorgehensweise sind häufig folgende grundlegenden Fragen von zentraler Bedeutung: Welchen Einfluss besitzen die Parameter meines Computermodells auf die Berechnungen? Wie robust ist mein Computermodell bezüglich Änderungen in Modellparametern? Wie passe ich Modellparameter an experimentelle Messdaten an? Gibt es Abhängigkeiten meiner Modellparameter untereinander? Wie lege ich mein technisches System aus? Wie plane ich mein nächstes Experiment so, dass Unsicherheiten in meinen Modellparametern minimal sind?
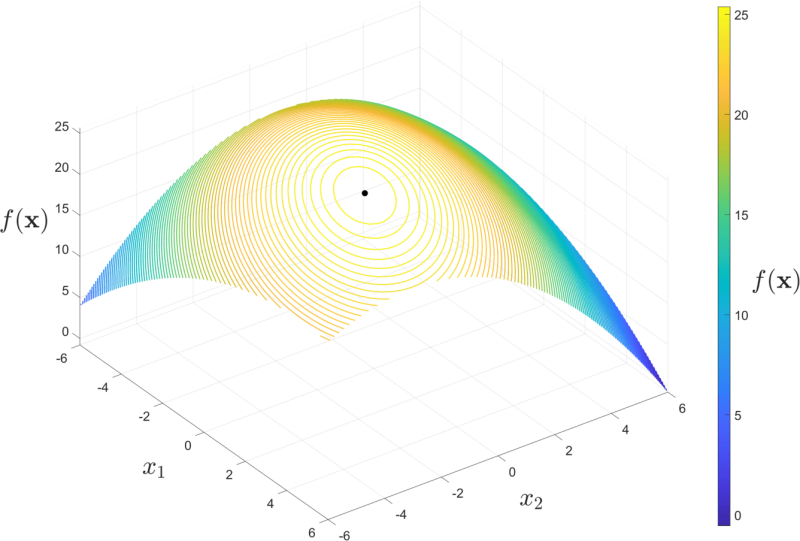
Verfahren zur Beantwortung solcher Fragestellungen beruhen wesentlich auf der Verfügbarkeit von Änderungsraten, die auch Ableitungen genannt werden. Ableitungen beantworten die Frage nach der Änderung einer Größe bei Variation eines Parameters. Im Gebirge beschreibt beispielsweise die Ableitung der geografischen Höhe nach dem Standort den Anstieg bzw. das Gefälle einer Landschaft. Eine genaue Information über Anstieg oder Gefälle ist oft hilfreich, etwa wenn man einen möglichst kurzen Weg zum nächsten Gipfel oder Tal sucht. In der folgenden Abbildung ist eine gebirgsähnliche Funktion f in Abhängigkeit von zwei Variablen x1 und x2 skizziert. Mit Farbe ist der Wert der Funktion gekennzeichnet. Die großen Funktionswerte entsprechen dem gelben Bereich und das Maximum der Funktion ist mit einem schwarzen Punkt dargestellt.
2D Funktion
Will man nun ein Verfahren entwickeln, welches das Maximum einer Funktion bestimmt, so stellt man sich einen Wanderer im Gebirge vor. Ein ungeübter Bergwanderer auf dem Weg zum Gipfelkreuz fragt einen in Richtung Tal entgegenkommenden Wandersmann: "Wie steil ist der Aufstieg?" Will er mit seinen begrenzten Kräften haushalten, dürfte er sich mit einer vagen Antwort wie "Es geht ziemlich bergauf" kaum zufriedengeben. Vielmehr wird ihn interessieren, wie stark es tatsächlich zahlenmäßig bergauf geht. Ableitungen würden hier nicht nur eine qualitative Information ("ziemlich bergauf") erlauben, sondern durch eine quantitative Angabe der Form "12.6 % Anstieg" einen echten Mehrwert darstellen.
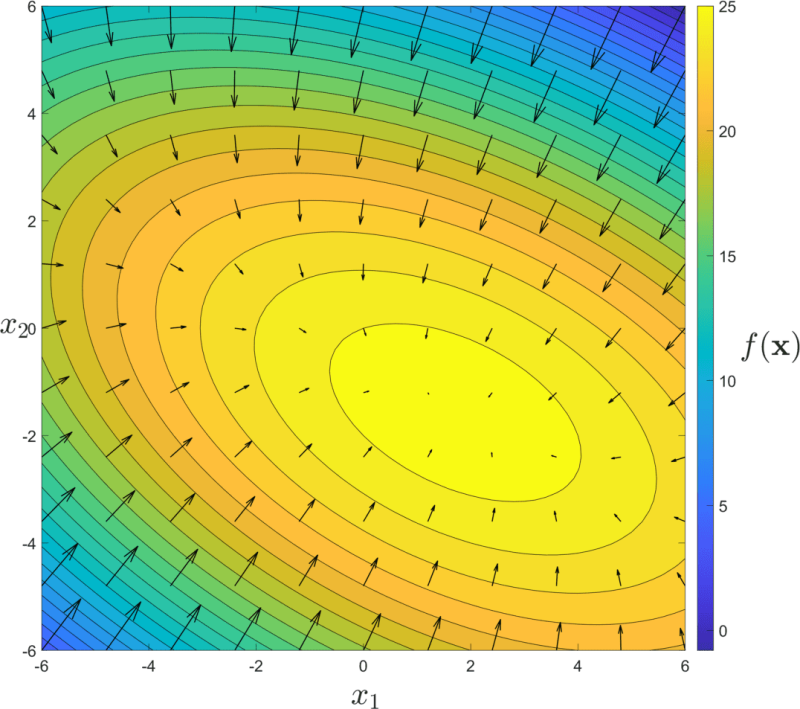
Ableitungen von skalarwertigen Funktion werden mit dem Fachbegriff "Gradienten" bezeichnet. Die Gradienten der Funktion aus der vorherigen Abbildung sind in der nun folgenden Abbildung als Pfeile dargestellt. Die Gradienten zeigen an jedem Ortspunkt in Richtung des steilsten Anstiegs. Zusätzlich wird der Betrag eines Gradientenvektors durch die Länge eines Pfeiles charakterisiert. Wie diese Abbildung zeigt, sind die Gradientenvektoren in der Nähe des Maximums sehr klein. Diese allgemeingültige Eigenschaft kann ausgenutzt werden, um effiziente Verfahren zur Bestimmung des Maximums (oder Minimums) einer Funktion zu entwerfen.
Funktionswerte einer 2 dimensionalen Funktion
Die Bestimmung der Gradienten einer gegebenen Funktion ist daher ein Kernelement von vielen Verfahren der mathematischen Optimierung. In der Praxis ist die Berechnung von Gradienten allerdings häufig ein schwieriges Problem, weil die zugrundeliegenden Funktionen oft als komplizierte Computerprogramme vorliegen. Will man beispielsweise die Geometrie eines Großraumflugzeuges wie des Airbus A380 so auslegen, dass dessen Auftrieb maximiert wird, benötigt man die Ableitungen eines Programms, das die zugrundeliegenden Gleichungen der Strömungsdynamik löst. Solche Programme können Millionen von Anweisungen enthalten und von unterschiedlichen Autoren über Jahrzehnte entwickelt worden sein.
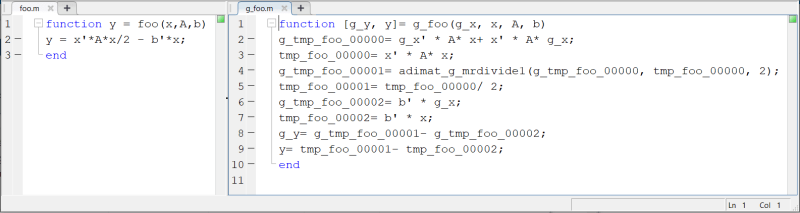
Die Berechnung der Ableitung von solchen komplizierten Funktionen erscheint auf den ersten Blick aussichtslos. Glücklicherweise bieten Techniken der Informatik an dieser Stelle einen Ausweg, der allerdings derzeit noch nicht bekannt genug ist. Unter dem Begriff "automatisches oder algorithmisches Differenzieren" versteht man eine Menge von Techniken zur Bestimmung von Ableitungen von Funktionen, die in der Form von Computerprogrammen vorliegen. Mithilfe dieser Techniken wird ein gegebenes Programm unter Verwendung von wohldefinierten Regeln in ein neues Programm transformiert. Auf diese Weise entstehen automatisch erzeugte Computerprogramme, die die Ableitungen einer vorgegebenen Funktion berechnen. Der Lehrstuhl für Advanced Computing entwickelt gemeinsam mit Wissenschaftlern der TU Darmstadt ein Software-Werkzeug zum automatischen Differenzieren für die Programmiersprache Matlab. Die folgende Abbildung zeigt im linken Teil ein Beispiel einer simplen Funktion, die in Form eines Matlab-Programms gegeben ist. Für eine gegebene Matrix A und zwei gegebenen Vektoren x und b berechnet diese Funktion den Wert y. Die rechte Seite zeigt das automatisch erzeugte Programm, welches die Ableitungen dieses Wertes y nach allen Einträgen des Vektors x berechnet.
Quelltext
Diese Techniken sind auf andere Programmiersprachen übertragbar und skalieren zu komplizierten Programmen mit Millionen Zeilen von Code. Weiterführende Informationen zum automatischem Differenzieren gibt das Portal www.autodiff.orgExterner Link, das an der FSU Jena betrieben wird.
H. Martin Bücker, Univ.-Prof. Dr.
Leiter Lehrstuhl Advanced Computing
Professur für Advanced Computing
